 ,
,  ,
, Le théorème de Kleene nous indique que les langages reconnaissables et les langages rationnels sont en réalité une seule et même classe de langages. La démonstration de ce théorème est une démonstration par induction. A la section précédente, nous avons aussi montré comment passer d'une expression rationnelle à un automate fini reconnaissant le même langage. En particulier, les deux premières méthodes (méthode intuitive et méthode de Thompson) sont proches de la démonstration par induction puisqu'il y a décomposition de l'expression et construction de l'automate en fonction des langages de base et des opérateurs utilisés. Ces méthodes permettent de prouver, qu'à une expression rationnelle, on peut faire correspondre un automate fini. Il est aussi possible de montrer la réciproque et d'en déduire des algorithmes effectuant cette opération.
Remarque : un intéret de cette transformation
est de faciliter l'implémentation d'un traitement décrit par un
automate fini. En effet, certains langages de programmation comme  ,
,  ,
, ![]() ,
, ![]() ...
possèdent des fonctions permettant de faire des traitements
décrits par des expressions rationnelles (souvent appelées
plutôt expressions régulières).
...
possèdent des fonctions permettant de faire des traitements
décrits par des expressions rationnelles (souvent appelées
plutôt expressions régulières).
La méthode de McNaughton & Yamada permet de prouver qu'un langage reconnaissable est rationnel. Cette démonstration se base sur la notion de langage entre deux états.
Soit T={A,Q,I={i},F, µ} un automate fini standard. L(T) désigne le langage reconnu par T et l(p,q) désigne le langage entre les états p et q. Alors, L(T) = ∪q∈F l(i,q).
L'objectif est de montrer que ∀,
p,q ∈ Q, l(p,q) ∈ Rat(A*)
et donc aussi L(T).
Il faut commencer par ordonner totalement les états en les numérotant de 1 à n (avec |q|=n). Ceci ne pose pas de problèmes car la numérotation des états n'a aucune influence sur la reconnaissance du langage.
Soit lk(i,j) (∀ i,j∈ Q, ∀ k ∈ [0,n]) l'ensemble des chemins (mots) permettant de passer de i à j sans passer par les états s > k.
Alors
l(i,j) = |
ln(i,j) si i≠ j |
| ln(i,j) ∪ {ε} si i = j |
Montrons que lk(i,j) ∈ Rat(A*) . Il suffit de procéder par induction :
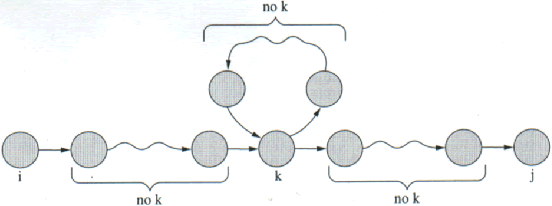
Par conséquent comme
l(i,j) = |
ln(i,j) si i≠ j |
| ln(i,j) ∪ {ε} si i = j |
l(i,j) ∈ Rat(A*) ∀ i,j∈ Q
De plus, comme L(T) = ∪q∈F l(i,q) et que l'union de langages rationnels est un langage rationnel alors L(T) ∈ Rat(A*)
CQFD !
De plus, l(i,j) ∈ Rat(A*) donc l(i,j) peut être décrit par une expression rationnelle rij
Donc L(T) = ∪q∈F l(i,q) est décrit par riq1 | ... |riqn avec qi ∈ F
Il est donc possible de construire une expression rationnelle à partir d'un automate fini. Il suffit de construire les matrices successives des li (p en lignes et q en colonnes).
L'algorithme fonctionne de la manière suivante : après avoir renuméroté les états, on regarde les langages en transition directe entre les différents états de l'automate (l0) puis les langages que l'on obtient en passant, en plus, par l'état 1 (l1) puis ceux passant, en plus, par l'état 2 (l2)... Lorsqu'il n'y a pas d'autres états à ajouter, s'est terminé ! Il suffit alors de prendre les langages entre un état initial et un état final. Lorsque ces deux états sont identiques, on ajoute alors ε.
Remarque : comme nous le verrons dans l'exemple suivant, cette méthode est extrêmement lourde à manipuler "à la main" (on préférera la méthode suivante). Par contre, elle est facile à implémenter.
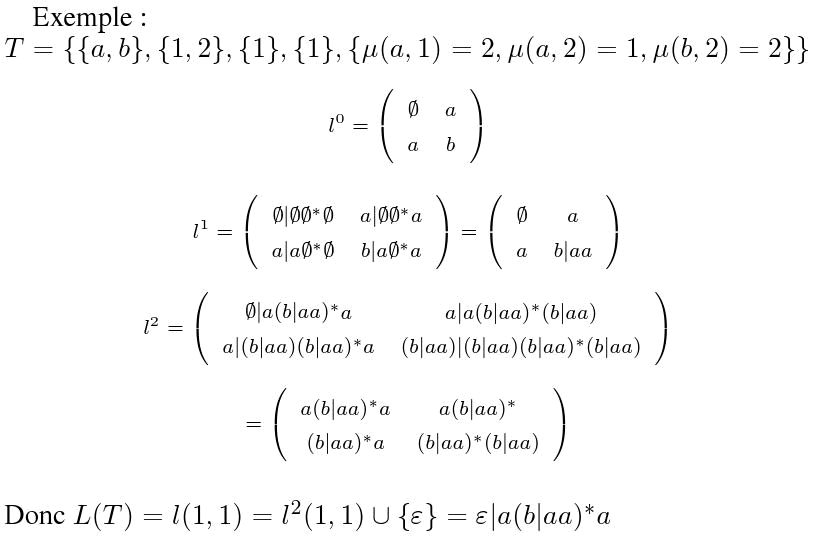
Et l'automate ne comporte que deux états !
Donc le langage reconnu par T est décrit par r1=ε | a(b|aa)*a
Une autre approche pour prouver qu'un langage reconnaissable est rationnel est de passer par la notion de langage droit d'un état. Là encore, nous obtenons l'expression rationnelle du langage.
Soit T={A,Q,I,F, µ} un automate fini ε-libre. L(T) = ∪i∈I LDT(i).
Si x ∈ LDT(q) alors :
Donc ∀ p ∈ Q, LDT(p) = ∪q∈Q Ep,qLDT(q) + δp
avec Ep,q={a : a ∈ A, µ(a,p)=q} ∈ Rat(A*) car fini (A est fini).
et δp=ε si p ∈ F, ∅ sinon
δp ∈ Rat(A*) (par définition - cas de base - des langages rationnels)
En appliquant cette équation pour chacun des états de l'automate, nous obtenons alors un système de n équations rationnelles (n=|Q|) à n inconnues où les inconnues sont les LDT(p) (notée Lp) et les coefficients sont des expressions rationnelles. La résolution d'un tel système s'effectue en utilisant principalement le lemme d'Arden. Cette résolution permet d'obtenir pour chaque Li une expression rationnelle décrivant LDT(i).
Le langage L(T) est alors : L(T) = ∪i∈ILi.
Reprenons l'exemple présenté pour la méthode précédente :
T = {{a,b}, {1,2}, {1}, {1}, {µ(a,1)=2, µ(a,2)=1, µ(b,2)=2}}.
La construction du système d'équations associé donne :
L1 = aL2 + 1 (car
l'état 1 est final)
L2 = bL2 + aL1
Qui se résoud de la manière suivante :
L2
= b*aL1 (grâce au lemme d'Arden)
L1 =
ab*aL1 + 1 = (ab*a)* (grâce au lemme
d'Arden)
L'expression rationnelle décrivant le langage est L1 car l'état 1 est le seul état initial. Donc L(T) est décrit par r2=(ab*a)*.
Notons que pour un même automate (T), McNaughton&Yamada (r1 = ε | a(b|aa)*a) et la résolution de système d'équations (r2 = (ab*a)*) ne donnent pas le même résultat mais ces deux expressions rationnelles décrivent bien le même langage (preuve) .
Remarque : avant de calculer le système d'équation associé à un automate, il est conseillé de l'émonder. En effet, tout état en moins réduit le système d'une équation et d'une inconnue sans pour autant changer le langage. Dans le cas où l'automate n'est pas émondé, il faut par exemple faire attention aux états stériles.
Prenons l'exemple suivant :
T = {{a,b}, {1,2,3,4}, {1}, {1}, {µ(a,1)=2, µ(b,1)=4, µ(b,2)=1, µ(a,2)=3, µ(b,3)=3}}.
La construction du système d'équations associé donne :
L1 = aL2 + bL4 + 1
L2 = bL1 + aL3
L3 = bL3 + ∅
L4 = ∅
d'où L3 = b*∅ = ∅
et donc : L2 = bL1 et L1 = aL2 + 1
L1 = abL1 + 1 = (ab)*
Pour terminer, nous allons présenter une méthode, plus "graphique", de transformation d'un AFN en une expression rationnelle appelée méthode d'élimination des états ou méthode BMC (pour Brzozowiski et McCluskey). Cette méthode utilise un graphe (appelé parfois "automate étendu") identique à l'AFN au départ mais qui, tout au long du traitement, pourra comporter des expressions rationnelles comme étiquette sur les arcs (ex-transitions).
L'automate d'origine sera supposé unitaire mais pas forcément déterministe ou ε-libre.
Pour T={A,Q,{i},F, µ}, la méthode est la suivante :
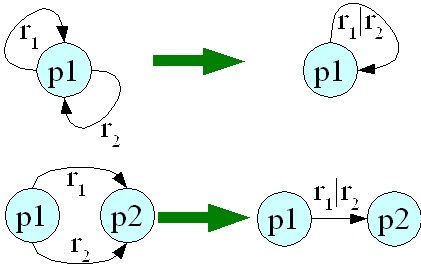
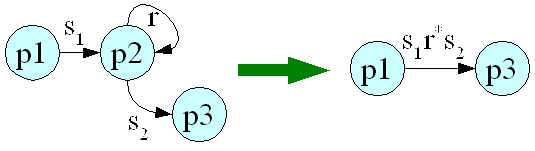
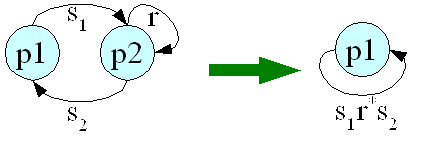
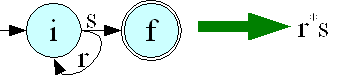
Lorsque plusieurs transitions entrent et sortent d'un état, alors pour le supprimer, il faut considérer toutes les combinaisons à trois états comprenant une transition entrante et une transition sortante.
Par exemple, soit l'automate suivant :
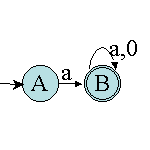
Nous obtenons alors les transformations suivantes :
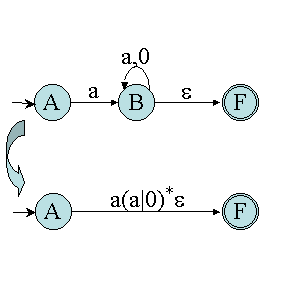
Nous pouvons en conclure que l'automate reconnaît le langage décrit par l'expression : a(a|0)*.
Prenons un autre exemple :
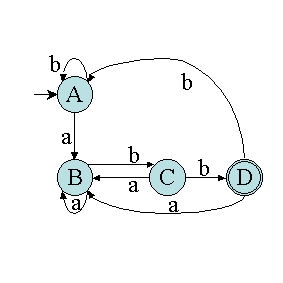
Nous obtenons alors en ajoutant un état final :
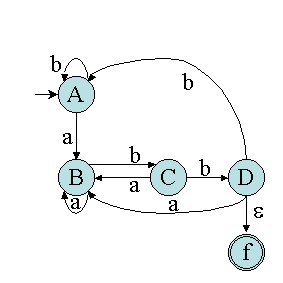
Puis nous obtenons les simplifications suivantes :
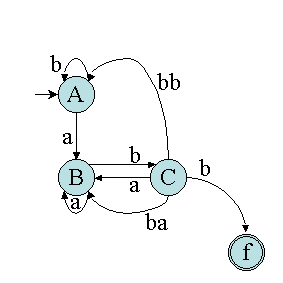
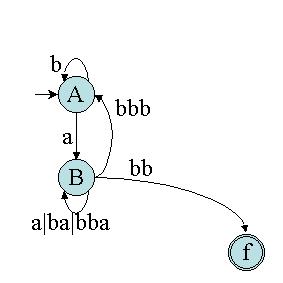
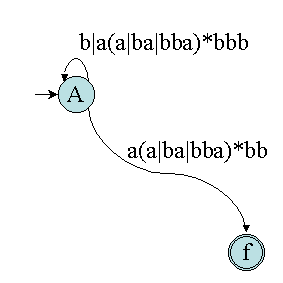
D'où l'expression suivante : (b|a(a|ba|bba)*bbb)*a(a|ba|bba)*bb
Noter que l'expression qui a été utilisée pour construire l'automate de départ était : (a|b)*abb !
Exercices et tests :
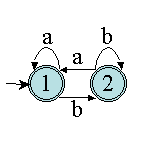
Exercice 4.1. Soit l'automate suivant sur l'alphabet {a,b} :
Exercice 4.2. Déterminer le langage reconnu par l'automate T={{a,b}, {1,2,3}, {1}, {1}, {µ(a,1)=1, µ(b,1)=2, µ(a,2)=3, µ(b,2)=1, µ(a,3)=2, µ(b,3)=3}} par la méthode de résolution de systèmes d'équations rationnelles.
Exercice 4.3. Soit l'automate fini suivant : T={{a,b,c}, {1,2,3,4}, {1,3}, {2,4}, {µ(b,1)=2, µ(b,1)=3, µ(a,2)=2, µ(a,2)=4, µ(c,3)=4, µ(c,4)=4}}.

mercredi, 17/12/03 10:41