Langage entre état
Un langage entre deux états quelconques q0 et q1 de T=(A, Q, I, F, μ) est défini par : lT(q0, q1) = {w | w ∈ A*, ∀ x ∈ A*, (wx,q0) —*/T→ (x,q1)}.
Les machines de Turing (et donc les AFNs), nous l'avons vu, sont aussi appelées "accepteurs" ("Language Acceptor") lorsqu'elles sont utilisées pour reconnaître un langage donné en Théorie de Langages. Un automate fini sert à reconnaître un langage bien particulier. Il est donc possible de définir le langage reconnu par un automate donné. Pour cela, nous utilisons les notions de langage entre deux états, de langage gauche et de langage droit.
Un langage entre deux états correspond aux différentes successions de symboles (aux différents mots) permettant de passer d'un état donné à un autre.
|
Un langage entre deux états quelconques q0 et q1 de T=(A, Q, I, F, μ) est défini par : lT(q0, q1) = {w | w ∈ A*, ∀ x ∈ A*, (wx,q0) —*/T→ (x,q1)}. |
Le langage gauche d'un état est l'ensemble des suites de symboles (l'ensemble des mots) permettant d'atteindre cet état à partir des états initiaux. Le langage droit d'un état est celui permettant, à partir de cet état, d'atteindre les états finaux.
Le langage gauche d'un état q ∈ Q d'un AFN T=(A, Q, I, F, μ) est donné par la fonction LGT : Q → A* où LGT(q) = ∪i∈I lT(i,q) = {w | w ∈ A*, x ∈ A*, ∃i ∈ I, (wx,i) —*/T→ (x,q)} Le langage droit d'un état q ∈ Q d'un AFN T=(A, Q, I, F, μ) est donné par la fonction LDT : Q → A* où LDT(q) = ∪f∈F lT(q,f) = {w | w ∈ A*, ∃f ∈ F, (w,q) —*/T→ (ε,f)}. |
Un langage reconnu par un AFN est donc l'ensemble des suites de symboles (l'ensemble des mots) permettant d'atteindre un état final à partir d'un état initial.
Un langage reconnu (accepté, défini) par un AFN T=(A, Q, I, F, μ) est donné par la fonction L : AFN → A* où L(T) = ∪f∈F LGT(f) = ∪i∈I LDT(i) = ∪i∈I,f∈F lT(i,f). L(T) est donc l'ensemble des chaînes acceptées par T, c'est-à-dire : L(T) = {w | w ∈ A*, ∃ f ∈ F, i ∈ I : (w,i) —*/T→ (ε,f)}. Un langage L sur un alphabet A est dit langage reconnaissable, noté L ∈ Rec(A*), s'il existe un automate fini T tel que L = L(T). |
Attention, un
langage est reconnaissable si l'on peut construire un AFN qui reconnait TOUS
les mots du langage et UNIQUEMENT les mots du langage.
Il est alors possible alors de comparer deux automates à partir des langages qu'ils reconnaissent.
|
Deux
automates sont équivalents s'ils
acceptent le même langage,
c'est-à-dire : |
Exercices et tests :
Exercice 5.1. Montrer que les langages suivants sont reconnaissables
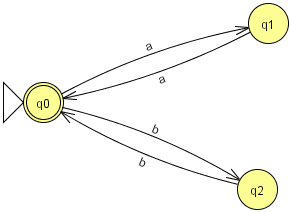
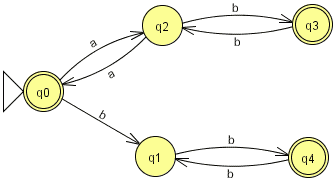
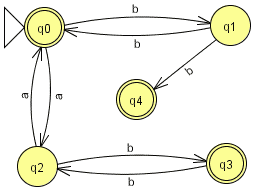
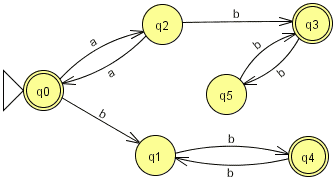
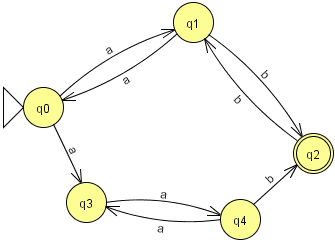
Exercice 5.2. Parmi les automates suivants, quel est celui reconnaissant les mots du langage {anbm | n mod 2 = m mod 2}, autrement dit le langage avec d'abord des "a" et ensuite des "b" et tel que le nombre de "a" et le nombre de "b" ont même parité (images issues de JFLAP) :
mardi, 25/11/03 11:38