4.
Classification des grammaires
De même que les expressions rationnelles permettent d'atteindre la classe
des langages rationnels (ou réguliers), différents types de grammaires
permettent d'atteindre différentes classes de langages. La classification
de N. Chomsky [Chomsky 56] se fonde sur
des contraintes concernant la forme des règles de dérivation.
Selon l'ordre croissant des contraintes, nous avons la classification suivante
:

Type de la grammaire |
Formes
des règles |
Type
0 : sans contraintes |
- x → y avec x ∈ V*×VN×V* et y ∈ V*. |
Type
1 : contextuelle
(context sensitive,
sensible au contexte) |
- x → y avec |x|≤|y|. |
Type
1 (bis) : contextuelle
Autre définition |
- xXy → xYy avec x, y ∈ V*, X ∈ VN et Y ∈
V+ tel que |Y| ≥ 1 (c'est-à-dire que X peut être
remplacé par Y dans le contexte xXy).
Habituellement, on introduit une exception à ces règles :
l'axiome, s'il n'est pas en partie droite d'une autre règle que celle
qui le définit, peut engendrer ε. Cette exception est aussi valable pour les types suivants |
Grammaires
"à structure de phrase" |
- Grammaires de type 1 telles que les règles x → y avec x
∈ VN+ et y ∈ V+. |
Type
2 : hors-contexte
(context free,
algébrique) |
- X → x avec X ∈ VN et x ∈ V+. |
Type 3 : linéaires
(régulières, d'états finis)
[à] droite (resp. [à] gauche) |
- uniquement : X → x1 | x2Y (resp. X →
x1 | Yx2) avec X, Y ∈ VN et x1
∈ VT+, x2 ∈ VT*.
|
Par exemple, une grammaire avec comme règles S → 0S | 1S | ε
est linéaire droite. Dans la section précédente, G0
et G4 sont de type 0, G1 est xde type 1, G2
est de type 2 et G3 est de type 3.
Les définitions rationnelles peuvent être
considérées comme des grammaires hors-contexte particulières
(si d1 est l'axiome et si ∀ i, i>1, di n'engendre pas ε).
La classification de Chomsky introduit
quatre classes de langage engendrées par les quatre types de grammaire.
Ces classes de langage satisfont la relation d'inclusion stricte suivante :
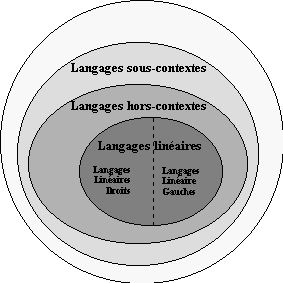
cl3 ⊂ cl2 ⊂ cl1 ⊂ cl0
Cette relation exprime entre autres que tout langage linéaire est hors-contexte
et qu'il existe des langages hors-contextes qui ne sont pas linéaires.
On a le même type de relation entre les autres classes de langages. Les
langages hors-contextes et linéaires sont les plus courants en informatique,
en particulier dans le cadre des langages de programmation; les algorithmes
de traitement pour ces deux classes sont les plus efficaces et les plus simples.
Dans le cadre de ce cours, nous étudierons plus particulièrement
le traitement des langages linéaires (en particulier à l'aide
des automates finis). Cependant nous présentons avant quelques outils
utiles sur les grammaires hors contexte (habituellement traité à
l'aide des automates à pile).
Exercices et tests :
Exercice 4.1. Pour chacune
des grammaires suivantes, donner leur type.
Gex1 = ({a,b,c}, {S}, S, {S → aSbSa
| c})
Gex2 = ({a,b,ch,d}, {S,A,B,C}, S, {S
→ BCaCbbA ; A → CaCbb | ε ; Ca → ba ; Cbb → da
; B → cha})
Gex3 = ({a,b}, {S,A}, S, {S → Aa | bA ; A → Sa | bS})

Exercice 4.2. Pour chacune
des grammaires suivantes, donner le langage engendré et préciser
le type de la grammaire :
Gex4 = ({a,b}, {S,A,B}, S, {S →
aAB ; B → SA ; Aa → Sab ; bB → a ; Ab → SBb})
Gex5 = ({/,\}, {S, U, V}, S, {S →
UAV | UV ; A → VSU | VU ; U → / ; V → \})

E. Desmontils (IUP-MIAGe de Nantes)
Last modified: Thu Jan 27 11:34:57 CET 2005


