3.
Définition des automates d'état fini
3.1. Présentation
Nous allons étudier en détail
un cas particulier de machine de Turing : les automates finis. Nous en donnerons
d'abord une définition précise. Nous verrons ensuite les différents
modes de représentation, leurs propriétés ainsi que les
algorithmes permettant de les utiliser.
La théorie des automates finis commence
avec l'article de S.C. Kleene [Kleene 56]
paru en 1956. Dans cet article tant de fois cité, Kleene démontre
le premier résultat de cette théorie. C'est à la fois le
premier dans l'ordre chronologique mais aussi dans l'ordre d'importance. Nous
verrons un peu plus loin ce théorème.
3.2. Définition
Un automate fini, très
souvent appelé "automate d'état fini"
[Perrin 95], ("finite-state machine",
"finite automaton", "Rabin-Scott Automaton"
[Ginzburg 68]) est une machine de Turing
dont le ruban se déplace toujours vers la gauche et case par case. Ce
ruban est infini à droite et fini à gauche. Par ailleurs, la tête
de lecture de la machine se contente de lire des symboles et n'effectue aucune
écriture.

Automate fini
Automate d'état fini
AFN
|
Un
automate fini (AFN) est composé
de la même manière que la machine
de Turing. Généralement non déterministe, son
comportement est cependant plus restreint. Il est défini par un
quintuplet (A, Q, I, F, μ) tel que :
- A est l'alphabet
(vocabulaire), ensemble fini, non vide de symboles ;
- Q est l'ensemble
des états possibles pour la machine (fini et non vide)
;
- I ⊆
Q est l'ensemble des états initiaux ou états de départ
;
- F ⊆
Q correspond aux états finaux ou états d'acceptation ;
- μ la
fonction de transition telle que μ : A ∪ {ε} ×
Q → Q. Pour la configuration courante d'état et de symbole,
μ(aj,qi)=qk signifie qu'on passe
dans l'état qk et que le ruban est déplacé
d'une case vers la gauche.
|
Remarques :
- Certains auteurs, dont [Watson
93a], définissent les automates par un 6-uplet (A, Q, E, I, F,
μ) en ajoutant un ensemble E des ε-transitions. Dans notre définition,
ces transitions sont définies par μ.
- Dans beaucoup de définitions,
l'ensemble I est réduit à un seul état.
- μ est une fonction partielle, car
elle n'est pas définie pour toutes les valeurs du domaine. Le plus
souvent, pour les couples (symbole, état) qui ne sont pas explicités,
elle est définie de la façon suivante : μ(a,q)=0 où
0 est un état qui n'existe pas. Ces transitions provoquent un arrêt
de l'automate ainsi qu'une erreur. L'état 0 peut être considéré
comme l'état d'erreur de l'automate.
- Les transitions peuvent être aussi
de la forme :
(ai, qj, qk) ≡ (ai, qj)
→ qk ≡ μ(ai, qj)= qk
avec ai ∈ A ; qj, qk ∈ Q ;
- Toujours à propos des transitions,
|(ai, qi, qk)| < 2
Au départ, une phrase construite
sur le vocabulaire de l'automate est inscrite sur le ruban d'entrée et
est entourée de symboles ε. L'unité centrale se trouve
dans un des états initiaux de I et la tête de lecture est placée
devant le symbole le plus à gauche de la phrase. A partir de cette position,
l'automate va exécuter son programme. Pour une configuration courante
(ai, qj), l'automate applique une transition μ(ai,
qj) → qk, passe alors dans l'état qk
et déplace le ruban d'une case vers la gauche. L'automate tel qu'il est
défini n'est pas forcément déterministe. Plusieurs transitions
concurrentes sont donc parfois applicables. L'automate s'exécute jusqu'à
ce qu'il arrive à une situation (at,qn) pour laquelle
il n'existe pas de transition permettant au programme de poursuivre son calcul.
Il suspend alors son exécution. Si la configuration finale est telle
que at = ε et qn ∈ F alors la phrase inscrite
sur le ruban est acceptée par l'automate. Dans tous
les autres cas, elle est refusée.
Remarque : Une façon utile de regarder
le non déterminisme est de considérer qu'il permet à un
automate de "formuler des hypothèses". Si, dans un état
donné, on ne sait pas quoi faire sur un certain caractère d'entrée,
il existe plusieurs possibilités pour le choix de l'état suivant.
Comme chaque chemin étiqueté par une chaîne de caractères
et conduisant à un état d'acceptation est interprété
comme acceptable, on fait confiance à l'automate non déterministe
dès qu'il fait une hypothèse juste, quel que soit le nombre d'hypothèses
fausses faites auparavant.
 Attention,
une transition d'un AFN ne peut concerner qu'un seul symbole de l'alphabet et
non pas un mot. Par contre, l'automate est indépendant des étiquettes
des états. Ils peuvent être numérotés de manière
continue ou pas, correspondre à des termes ayant un sens dans le langage
courant...
Attention,
une transition d'un AFN ne peut concerner qu'un seul symbole de l'alphabet et
non pas un mot. Par contre, l'automate est indépendant des étiquettes
des états. Ils peuvent être numérotés de manière
continue ou pas, correspondre à des termes ayant un sens dans le langage
courant...
3.2. Représentation des AFN
Les automates, et en particulier leur fonction de transition, peuvent être
représentés de plusieurs manières : par des graphes orientés
ou des représentations matricielles.
Prenons comme exemple l'automate T={{a,b,c}, {1}, {6,9}, μ}. Soit μ sa
fonction de transition :
- µ(a,1) = 2 ; µ(b,1) = 4 ; µ(a,2) = 5 ; µ(b,2) =
3 ; µ(c,2) = 2 ; µ(a,3) = 6 ; µ(b,3) = 4 ; µ(c,3)
= 9 ; µ(c,4) = 5 ; µ(a,5) = 5 ; µ(a,5) = 6 ; µ(c,7)
= 4
La fonction de transition est très souvent représentée
par une "table de transition" (parfois aussi appelée "matrice
de transition", "flow table" en anglais). Cette représentation
est très commode du point de vue de l'implémentation informatique
des AFNs. Les tables de transition sont des tableaux (ou des matrices) dont
les colonnes correspondent aux symboles et les lignes aux états. La cellule
(li,cj) indique les transitions (ai, qj)
→ qk. L'AFN étant susceptible d'être non déterministe,
plusieurs états peuvent être présents dans une cellule (li,cj).
Les symboles ne donnant aucune transition depuis un noeud dans un certain état
sont alors à "0" (transition vers un état inexistant).
Cet état correspond à un état d'erreur. C'est cette forme
qui est la plus souvent utilisée en programmation. Si on reprend l'AFN
servant d'exemple, nous avons alors la table suivante :
μ |
a |
b |
c |
1 |
2 |
4 |
0 |
2 |
5 |
3 |
2 |
3 |
6 |
4 |
9 |
4 |
0 |
0 |
5 |
5 |
5,6 |
0 |
0 |
6 |
0 |
0 |
0 |
7 |
0 |
0 |
4 |
8 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
Un AFN peut être aussi représenté par un graphe orienté
et valué, appelé "diagramme de transition" ou "graphe
de transition". Les noeuds correspondent aux états et les arcs représentent
les transitions possibles (calculées par la fonction de transition) entre
les états. Ces arcs sont étiquetés par le symbole permettant
cette transition. Les états initiaux sont représentés par
un noeud possédant une flèche entrante sans origine. Un état
final est représenté par un noeud doublement cerclé.
L'automate T, présenté précédemment, peut être
représenté par le graphe suivant :
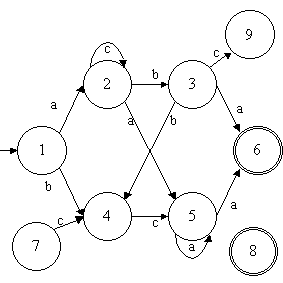
On observant cet automate T, de manière intuitive, on peut noter que
certains états ne sont pas particulièrement utiles. Prenons d'abord
l'état 7. Cet état n'intervient que dans une seule transition
(de 7 vers 4). Aucune transition n'est "dirigée" vers 7. Cela
signifie que la machine de Turing ne pourra jamais se trouver en l'état
7. Par conséquent, cet état peut être supprimé (ainsi
que la transition de 7 vers 4). Pour l'état 8, c'est pire puisqu'il est
totalement isolé. Il peut donc lui aussi être supprimé.
Enfin, avec l'état 9, la situation est un peu différente mais
le résultat sera le même. Lorsque la machine sera dans l'état
9, plus aucune transition n'étant exploitable, elle sera forcément
en échec. Donc, prendre la transition de 3 vers 9 sur "c" sera
forcément un échec. Si on supprime 9 et cette dernière
transition, le résultat sera totalement identique, c'est-à-dire
que étant sur 3, si le ruban est sur un "c", aucune transition
ne sera exploitable et donc la machine se mettra aussi en échec. En conclusion,
les états 7, 8 et 9 ainsi que les transitions associées peuvent
être supprimés. Nous obtenons alors le tableau et le diagramme
suivants :
μ |
a |
b |
c |
1 |
2 |
4 |
0 |
2 |
5 |
3 |
2 |
3 |
6 |
4 |
0 |
4 |
0 |
0 |
5 |
5 |
5,6 |
0 |
0 |
6 |
0 |
0 |
0 |
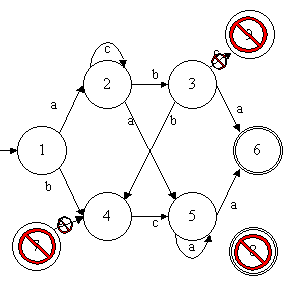
Nous verrons dans le suite que ce procédé de simplification d'automates
peut être automatisé. Nous verrons les notions associées
(état puit, source, accessible...) et les algorithmes adéquats
(élagage...). Nous irons même plus loin en fusionnant les états
jouant le même rôle.
Il existe aussi d'autres représentations possibles comme des matrices
binaires associées à chacun des symboles...
Remarque. Dans certains cas, il est plus facile de représenter un groupe
de transitions par une notation ensembliste. Par exemple, supposons que pour
un état donné qi, nous avons soit un passage à
l'état qj pour les symboles ap et aq
soit une conservation de l'état courant pour les autres symboles de l'alphabet
A. Ce type de transition s'écrit : (ap, qi) →
qj ; (aq, qi) → qj ; (a1,
qi) → qi ; (a2, qi) →
qi ; ... Soit : (aj,qi) → qi,
∀ i ∉ {p,q}. Pour simplifier l'écriture, nous aurons : ({ap,
aq}, qi) → qj ; (A-{ap, aq},
qi) → q_i.
Plus généralement, les symboles peuvent être regroupés
sous différentes classes et l'automate possède des transitions
en fonction de ces classes. Nous retrouvons ici la même simplification
que nous avions utilisée pour les expressions rationnelles (nous verrons
que cette similitude n'est pas un hasard).
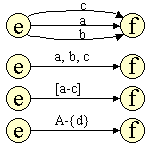
Cette simplification dans la syntaxe se répercute aussi au niveau du
diagramme d'états. Les quatre notations suivantes sont équivalentes
(en considérant un automate sur l'alphabet {a,b,c,d}) :
 Mais
attention, dans tous les cas, une transition ne concerne qu'UN SYMBOLE de l'alphabet.
Les notations précédentes permettent simplement de simplifier
la représentation de l'automate. Dans les 4, les trois dernières
sont des "simplifications visuelles" de la première.
Mais
attention, dans tous les cas, une transition ne concerne qu'UN SYMBOLE de l'alphabet.
Les notations précédentes permettent simplement de simplifier
la représentation de l'automate. Dans les 4, les trois dernières
sont des "simplifications visuelles" de la première.
3.3. Exemple d'exécution d'un AFN
Nous avons vu qu'un automate fini est un cas particulier de machine de Turing.
Il est donc possible de simuler le fonctionnement de cette machine. Pour cela,
le plus courant est d'utiliser le graphe des transitions. Prenons par exemple
l'automate T1 = {{1,2,3,4,5,6},{1},{6}, {(a,1) → 2, (b,1) →
4, (a,2) → 5, (c,2) → 2, (b,2) → 3, (a,3) → 6, (b,3) →
4, (c,4) → 5, (a,5) → 5, (a,5) → 6}} et étudions le mot
"accaa" sur cet automate. N'ayant qu'un seul état initial,
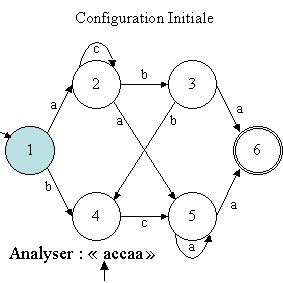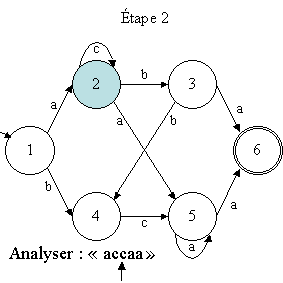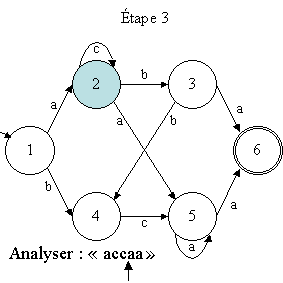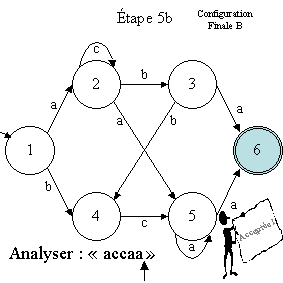
la configuration initiale
est schématisé par le graphe suivant (en bleu, l'état courant
de la machine ; la flèche indique la position de la tête de lecture
de la machine sur le mot) :
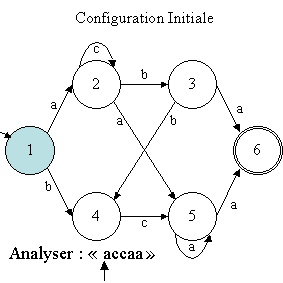
A partir de cette configuration initiale (état 1, symbole "a"),
la seule transition possible pour faire évoluer la machine est celle
de 1 vers 2 sur "a". Donc, la machine passe dans la configuration
(état 2, symbole "c"). De même, à nouveau, la
seule transition possible est celle de 2 vers 2 sur "c". Donc, la
machine passe dans la configuration
(état 2, symbole "c"). De nouveau, la seule transition possible
est celle de 2 vers 2 sur "c". Donc, la machine passe dans la configuration
(état 2, symbole "a"). Maintenant, la seule transition possible
est celle de 2 vers 5 sur "a". Donc, la machine passe dans la configuration
suivante (état 5, symbole "a").
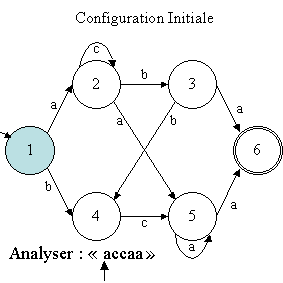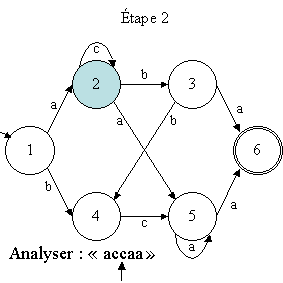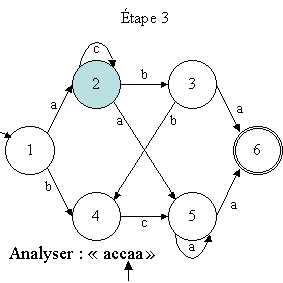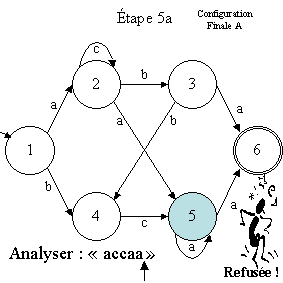
La configuration courante nous pose un problème. En effet, étant
dans la configuration (état 5, symbole "a"), deux transitions
peuvent être exploitées : celle de 5 vers 5 sur "a" ou
celle de 5 vers 6 sur "a". Cette situation est une situation de non-déterminisme.
Il faut donc choisir une transition en prévoyant éventuellement
de revenir dans cette configuration pour en reprendre une autre. Prenons donc
la transition de 5 vers 5. La machine passe alors dans la configuration (état
5, symbole "ε"). Or, 5 n'est pas un état final. La
machine est donc dans une situation d'échec (plus de symbole et état
non final).
Il convient donc de revenir en arrière pour reprendre la transition
de 5 vers 6 dans la configuration (état 5, symbole "a"). La
machine passe alors dans la configuration
finale (état 6, symbole "ε").
Le mot proposé "accaa" est alors accepté par l'automate
T1. Il en est de même pour les mots "aba", "bcaaa",
"acba", acbbcaaa"... Par contre, pour le mot "abaa"
n'est pas accepté. En effet, au bout d'un certain nombre d'étapes,
la machine se retrouve dans la configuration (état 6, symbole "a").
A ce moment, plus aucune transition n'est exploitable et il reste un symbole
à étudier. La machine est en échec et le mot est refusé.
De même, pour "abbb", la machine va se retrouver dans la configuration
(état 4, symbole "b"). Dans cette configuration, à partir
de 4, aucune transition sur "b" n'est disponible.
3.4. Configuration et action
Pour pouvoir exprimer de manière plus formelle le déroulement
d'un programme sur un automate fini, il est nécessaire d'introduire les
notions de configuration et d'action.

Configuration d'un AFN
Configuration d'arrêt
Configuration non-déterministe
Configuration déterministe
|
Si
T=(A, Q, I, F, μ) est un AFN, alors tout couple (a, q) avec a ∈
A* et q ∈ Q est une configuration de T. Contrairement à la
notion de configuration
d'une machine de Turing, a n'est pas un symbole mais un mot contenant
les symboles restant à parcourir.
Une
configuration d'arrêt est une configuration soit
de la forme (ε, q) ∀q ∈ Q, ∀a ∈ A* soit
de la forme (a, q) ∀q ∈ Q telle qu'il n'existe pas de transition
(a, q) → q' ∀q' ∈ Q, ∀a ∈ A* .
Il existe trois ensembles de
configurations particulières :
- les
configurations (a, qI) ∀a ∈ A* et qI
∈ I appelées configurations initiales ou
configurations de départ ;
- les
configurations d'arrêt de la forme (ε, qF)
avec qF ∈ F appelées configurations finales
ou configurations terminales.
- les
autres configurations appelées configurations intermédaires.
Une
configuration non déterministe est une configuration
à partir de laquelle plusieurs transitions sont possibles. Dans
le cas contraire, la configuration est dite configuration déterministe. |
Les machines exécutant un automate fini qui, pour un mot m, terminent
dans une configuration d'arrêt qui est une configuration finale sont en
situation d'acceptation (le mot m est accepté par l'automate). Dans tous
les autres cas de configuration d'arrêt, la reconnaissance échoue
(le mot m est rejeté). En cas de non déterminisme, un mot est
reconnu s'il existe au moins une configuration finale. Par contre, si toutes
les configurations d'arrêt ne sont pas finales, la reconnaissance échoue.
Exemples, avec T1 :
- ("accaa", 1) est une configuration initiale ;
- (ε, 6) est une configuration finale ;
- ("caa", 2) est une configuration intermédiaire.
Une action représente le passage d'une configuration donnée d'un
AFN à une autre par l'application d'une transition de l'automate. Bien
évidemment, pour les AFNs, il peut exister plusieurs actions différentes
pour une même configuration de départ (non déterminisme).

Action
Calcul
|
Une
action (ou un calcul, un déplacement)
de l'automate T=(A, Q, I, F, μ) est représentée par une
relation binaire sur les configurations notée —T→ ou
—1/T→ (→ s'il n'y a pas d'ambiguïté sur l'automate).
Alors la transition μ(a, qi)=qj peut s'écrire
(aw, qi) —1/T→ (w, qj).
On dit que C —0/T→ C'
si et seulement si C=C' et C —k/T→ Ck, k ≥ 1
si et seulement si ∃ C1, ..., Ck-1 tels que
Ci —T→ Ci+1 ∀ i, 0 ≤ i <
k et C0 = C |
Notations : C —+/T→ C' signifie C —k/T→ C' avec k ≥
1 et C —*/T→ C' signifie C —k/T→ C' avec k ≥ 0.

suite d'actions
chemin d'actions
|
Nous
appellerons suite d'actions (ou de configurations) ou
chemin d'actions les différentes actions consécutives
permettant de passer d'une configuration à une autre.
|
Par exemple, si on reprend l'automate T1 avec le mot "accaa", nous
obtenons les suites d'actions suivantes :
- (« accaa »,1) → (« ccaa »,2)
→ (« caa »,2) → (« aa »,2)
→ (« a »,5) configuration non-déterministe
:
- (« a »,5) → (ε,5) cette configuration
d'arrêt n'étant pas une configuration finale, le mot n'est
pas, pour l'instant, reconnu ;
- (« a »,5) → (ε,6) cette configuration
d'arrêt étant une configuration finale, le mot est reconnu.
Donc (« accaa »,1) —*/T1→ (ε,6)
(OK) et (« accaa »,1) —*/T1→ (ε,5)
(ECHEC)
Remarques :
- —+/T→ est la fermeture transitive de —T→ et —*/T→
est la fermeture réflexive et transitive de —T→.
- Parfois, il est possible de trouver l'utilisation d'une fonction partielle
récursive μ* définie à partir de la fonction de transition
μ sur A* × Q → Q telle que : μ*(ε,q)=q et μ*(aw,q)
= μ*(w,μ(a,q)).
Cette fonction est équivalente à la notion d'action : avec a
∈ A et w ∈ A*,
μ*(aw,q) = q' ≡ (aw,q) —1/T→ (w,q')
et μ*(w,I) = qf ≡ (w,I) —*/T→ (ε,qf).
Exercices et tests :
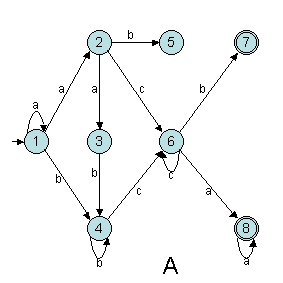
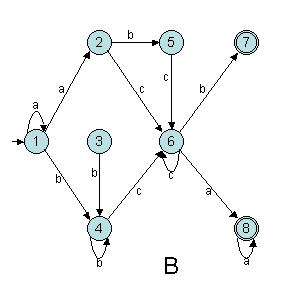
Exercice 3.1. Donnez toutes
les suites d'actions possibles pour chacun des mots suivants avec les automates
finis A et B (figures ci-dessous, alphabet {a,b,c}) et en déduire s'ils
sont reconnus : "ε", "a", "aab", "bcb",
"abca", "acac" et "aabbcb".

Exercice 3.2. Donner les automates
finis (alphabet, liste des états, états initiaux, états
finaux et transitions sous forme de table ou de diagramme) qui reconnaissent
les mots suivants :
- les mots terminés par "er", "é", "ée",
"és" et "ées" ;

- les mots contenant au moins deux "a" sur l'alphabet {a,b,c}
:
- consécutifs
- par forcément consécutifs

Exercice 3.3. Décrire
les mots reconnus par les automates suivants :





Exercice 3.4. Écrire un programme permettant de simuler le fonctionnement d'une machine de Turing basée
sur un AFD :
- Proposer l'algorithme général de reconnaissance par un automate
d'état fini déterministe quelconque dont le nombre d'états
ne dépasse pas 50 états et le nombre de symboles est limité aussi à 50.
 .
.
- Étudier l'automate suivant :
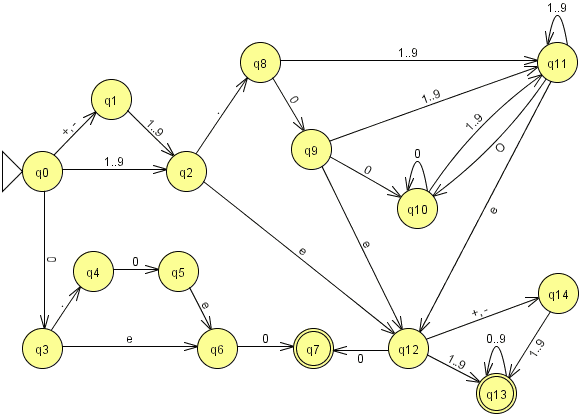
- Quel langage reconnaît-il ?
- Appliquer l'algorithme proposé en 1 à cet automate (l'automate
sera "en dur" dans le programme ou chargé à partir
d'un fichier) pour obtenir un programme permettant de reconnaitre les mots
du langage décrit par l'automate.

Exercice 3.5. Donner les automates
finis qui reconnaissent les mots des langages suivants sur le vocabulaire {a,b}
:
- le langage des mots avec un nombre pair de "a" et un nombre
impair de "b" ;

- le langage des mots ne contenant pas deux occurrences de "a"
successives.


Exercice 3.6. Donner un automate
reconnaissant le langage dont les mots sont des entiers multiples de 3 ({w
∈ A* tq w mod 3 = 0}).

jeudi, 27/05/04 14:12
![]()